Spatial Smoothing
- Details
- Category: Pre-Processing
- Last Updated: 09 April 2018
- Published: 09 April 2018
- Hits: 24159
1. Theoretical Background
Spatial smoothing means that data points are averaged with their neighbours. This has the effect of a low pass filter meaning that high frequencies of the signal are removed from the data while enhancing low frequencies. The result is that sharp "edges" of the images are blurred and spatial correlation within the data is more pronounced (see figure below).
The approach of spatial smoothing is commonly used in fMRI studies and is justified by the fact that fMRI data inherently show spatial correlations due to functional similarities of adjacent brain regions and the blurring of the vascular system.
The standard procedure of spatial smoothing is employed by convolving the fMRI signal with a Gaussian function of a specific width.This so called Gaussian kernel is a kernel with the shape of a normal distribution curve. In the figure below you can see a standard Gaussian with a mean of 0 and a standard deviation of 1.
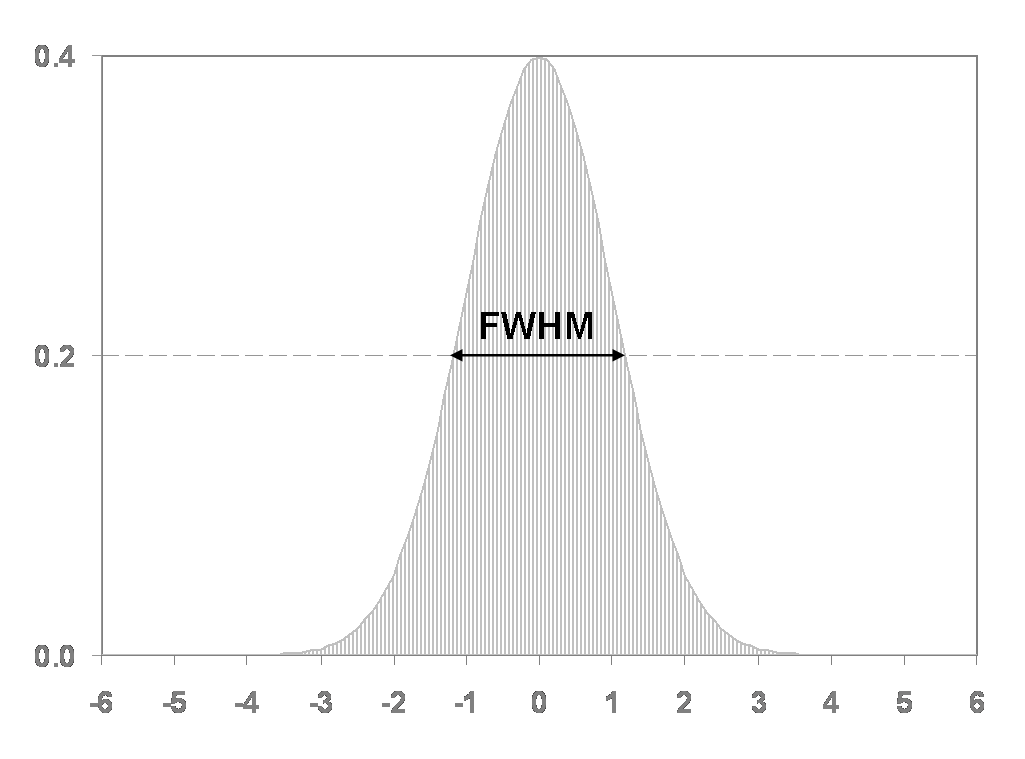
The size of the Gaussian kernel defines the "width" of the curve which determines in turn how much the data is smoothed. The width is not expressed in terms of the standard deviation σ, as customary in statistics, but with the Full Width at Half Maximum (FWHM). In this case the FWHM would be 2.35: The maximum of this curve is y = 0.4 at x = 0. The half maximum is y = 0.2 at x = -1.175 and at x = 1.175. Therefore, the full width of the curve at the point of the half maximum is about 2.35. Nevertheless, the FWHM is also related to the standard deviation σ as follows: FWHM = σ √(8 ln(2)).
There are several benefits associated with the application of spatial smoothing:
Improvement of the signal to noise ratio (SNR) => Increasing sensitivity
According to the matched filter theorem, the SNR reaches its maximum when the filter width matches the expected signal width. This, in turn, is of course dependent on the experimental design and the functional brain areas under investigation, e.g. Do you expect a narrow signal in the thalamus versus more extensive activations in the occipital lobe? Therefore, if a signal with a FWHM of 8 mm is expected the applied kernel size should be 8 mm as well.
Improving validity of the statistical tests by making the error distribution more normal
Most parametric tests assume normal error distributions and according to the central limit theorem the distribution of an average tends to be normal with a sufficiently large number of independent observations being averaged.
Accommodation of anatomical and functional variations between subjects
In multi-subject studies, individual brains are coregistered to each other to establish spatial correspondence between the different brains. Still, because of the substantial variation in individual brains, activated areas are rarely represented in exactly the same voxels. To increase the overlap of activated brain regions across subjects smoothing can be applied.
However, there are also some drawbacks which have to be carefully considered when specifying whether and to which extent spatially smoothing has to be applied:
Reduction of spatial resolution of the data
Spatial smoothing results always in reduced spatial resolution of the data. Therefore, it is important to decide whether a precise localization of the activations is important. However, even worse, if the filter width is set too small, there is practically no positive effect on the SNR while the spatial resolution is reduced.
Edge Artifacts
Along the edges of the brain, brain voxels are smoothed with non-brain voxels, resulting in a dark ring around the brain which might be mistaken for hypoactivity.
Merging
If activation peaks are less than twice the FWHM apart they are detected as a single activation rather than two separated ones.
Extinction
If the filter width is set too large, especially small meaningful activations might be attenuated below the significance threshold.
Mislocalization of activation peaks
As presented by Mikl and colleagues (2008) spatial smoothing almost unavoidably results in shifts of activation peaks. Therefore, as already mentioned above, it is crucial to decide what amount of spatial accuracy is required.
2. Spatial Smoothing in BrainVoyager QX
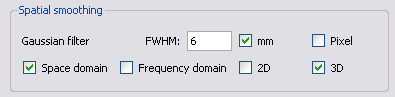
After BrainVoyager has finished spatial smoothing a new FMR is created whose file name is characterized by the options you used for filtering the data: "SD" for space domain versus "FD" for frequency domain, "3D" versus "2D", "SS" for spatial smoothing and the size of the filter kernel expressed in millimeter "mm" or pixels "px".
3. Comments on the Choice of the Kernel Size
Oversimplified, for single-subject analyses only modest filter sizes should be applied (about 4 mm), while for multi-subject analyses wider filters are reasonable to account for the intersubject-variability (about 6 -10 mm). However, to exploit the full spatial resolution of the data it is recommended to apply spatial smoothing only after having run single-subject analyses with no or only modest filter widths.
Furthermore, it is important to take into account that different preprocessing steps, like motion correction and creation of VTC files might also induce smoothing effects on the data depending on the interpolation method used. For example trilinear interpolation (often used because of its fast computation advantage) has the side-effect of “blurring” the data.
In sum, different factors have to be considered carefully, before deciding on the optimal kernel size.
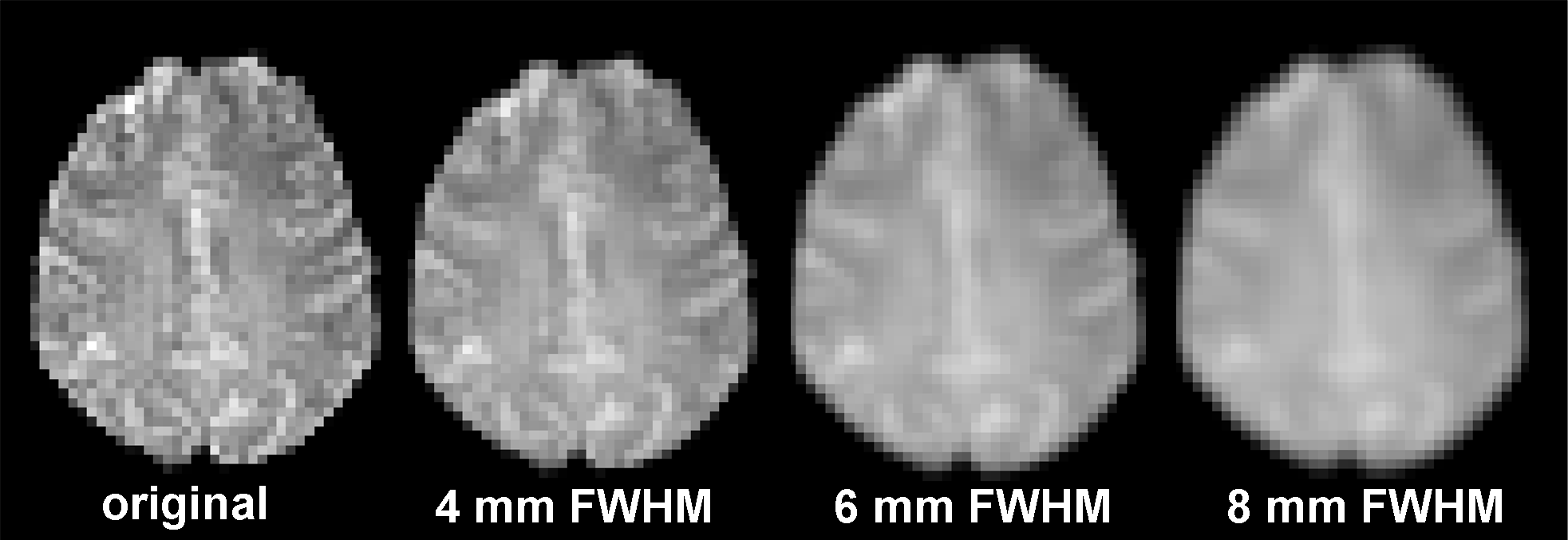
In the figures below the effect of different smoothing kernels on the amount of significant activations is nicely visible (with the same statistical threshold):
No Smoothing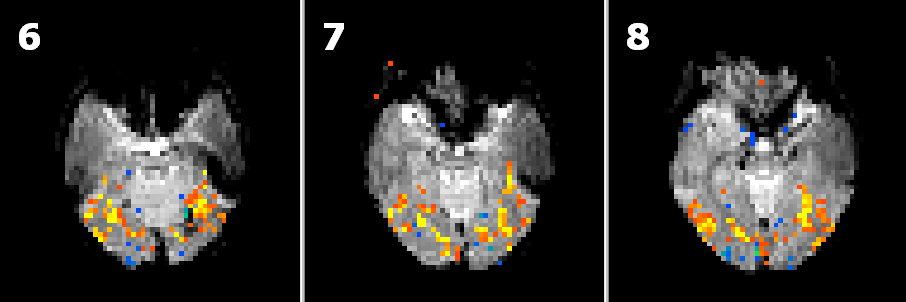
4 mm FWHM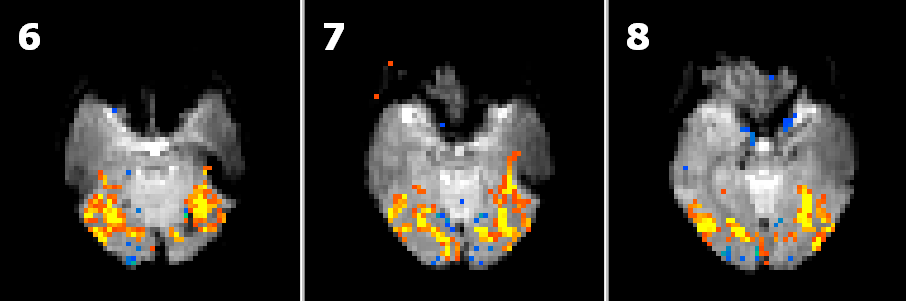
6 mm FWHM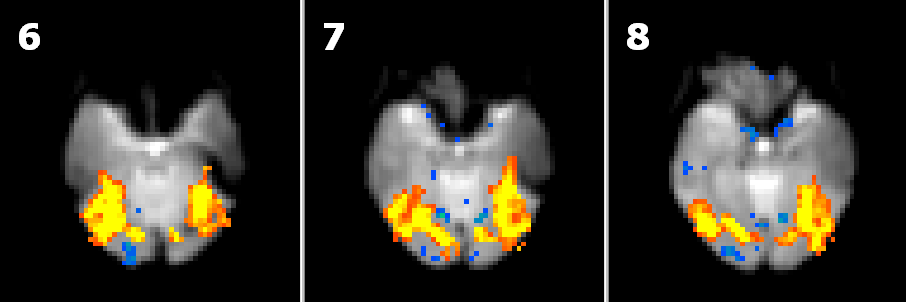
8 mm FWHM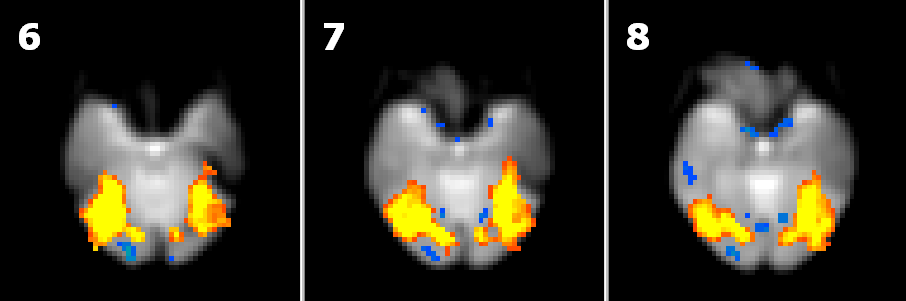
Note: The AMR is detached in all four versions of this functional data set, otherwise you would not see the difference in the blurring factor!
References and Suggested Readings
Worsley KJ, Marrett S, Neelin P, Evans AC. Searching scale space for activation in PET images. Hum Brain Mapp 1996; 4: 74 - 90. (theoretical background)
Mikl M, Mareček R, Hluštik P, Pavlicová M, Drastich A, Chlebus P, Brázdil M, Krupa P. Effects of spatial smoothing on fMRI group inferences. Magn Reson Imaging 2008; 26: 490 - 503. (practical considerations)
